Climb Speeds

Aircraft have different climbing speeds.  One is appropriate for getting the aircraft up to altitude as quickly as possible and the other is for gaining the most altitude in the least amount of lateral distance.  There is another speed, referred to as “cruise climb.”  Pilots have to know which climb speed is appropriate for different situations.

Vy is located at the maximum distance between the power required and the power available curves.

To define further the two most important speeds, best-rate of climb (Vy) and best-angle of climb (Vx), pilots need to understand how they are used.  Vy is the speed a pilot would use to get the airplane to altitude in the least amount of time.  Vx, on the other hand, allows the airplane to climb quickly in short distance to get the airplane over a nearby obstacle.

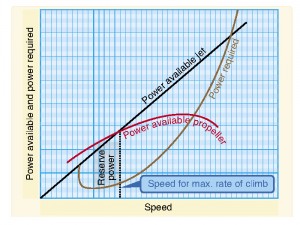
Vy is the speed at which there is the greatest surplus of power for the airplane.  Plotted out, it is the greatest distance between the power available curve and the power required curve.  The greater the distance, the greater the climb rate.

Another way of seeing this is mathematically by the formula,

ROC = (exhp x 33,000) / W

where ROC is the rate of climb in feet per minute, exhp is excess horsepower, and W is the gross weight of the aircraft.  What this formula tells us is that the bigger the engine, the more excess horsepower, and therefore, the higher climb rate.  Additionally, from the formula, you can see that rate of climb will increase with decreased aircraft weight.

As the airplane climbs to higher density altitudes, the actual best-rate of climb speed will change.  This is because the maximum power available curve will shift down and to the left with a gain in altitude because of a loss of power due to the thinner air.  Consequently, the best-rate of climb will decrease with a gain in altitude.

Conversely, the best-angle of climb speed decreases as the aircraft gains altitude.  If you plot rate of climb against velocity, the curve would be steep on the low end, the high point would be at Vy, and on the right side, the slope would be a shallow.  You can determine Vx by drawing a straight line from the tangent to the intersection of the rate of climb curve.

As the airplane gains altitude and the powerplant(s) lose power due to density altitude, the rate of climb curve will also shift down.  This will result in a natural increase in Vx.

The absolute ceiling is where Vy and Vx meet.

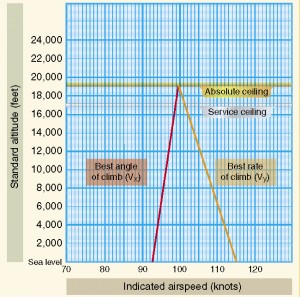
Now, we will talk about the definition of ceilings.  Most pilots know that the service ceiling of an aircraft is where the Vy rate of climb with full power is only 100 feet per minute.  The absolute ceiling is the point at which with full power, the aircraft can no longer climb.

Here is the interesting thing about the absolute ceiling: it is the intersection of Vy and Vx.  Plotting the two climb speeds, as Vy decreases and Vx increases, the two create a “tepee.”  The apex of the tepee is the absolute altitude.  At this juncture, pilot cannot increase pitch to climb; he is already at Vx.  He cannot increase airspeed to Vy either.  Consequently, the airplane can no longer climb.

Now that you have a basic understanding of the theory behind climb speeds, tomorrow we will discuss technique.

-30-

© 2011 J. Clark

• Tweet
• Pin It